Cryptography - Euclidean Algorithm

Introduction #

• In the previous blog, we did a general introduction to cryptography and the various important libraries and techniques for handling encrypted data with python.
• We introduce some basic math concepts in this blog, where we talk about GCD and the euclidean algorithm, its extended version and how to form recursive algorithms in python for them.

Why should you understand these concepts? #

• As we move into public key cryptography, all these concepts form a fundamental basis for understanding cryptosystems and cryptographic attacks. Some of the computations may be a bit confusing at first but grasping the logic behind these math algorithms will be important for you as we move forward.

Greatest Common Divisor (GCD) #

• Let us begin by defining these 2 terms:

  1. Factors - a number that divides another number evenly. i.e if 2 is a factor of 10, then 2 can divide 10 into 5 equal parts
  2. Common Factors - if the factor of a number is the factor of another number, then it is said to be a common factor i.e if 2 is a factor of 10 and 4, then 2 is said to be a common factor

• GCD is then the largest common factor of 2 or more positive integers

• Suppose we have 2 integers a=12, b=18, the factors of a are 2,3,4,6 while the factors of b are 2,3,6,9

• The greatest common divisor of the 2 would be 6

Euclidean’s Algorithm #

• Also known as Euclid’s algorithm, this is an efficient method of computing the GCD between 2 numbers.
• The algorithm is based on the following GCD property:

  • If we have 2 numbers, the GCD of the numbers does not change if the larger number is replaced by its remainder when divided by the smaller of the two

    i.e if a > b then GCD(a,b) = GCD(b,a%b)

Point to note

• Our operations will be expressed as follows

• For example, if we divide 48 by 6, we can express this as:

  48 ÷ 6 = 8 + 0

  48 - dividend

  6 - divider

  8 - quotient

  0 - remainder

• Rewrite in terms of the formula

48 = 8 * 6 + 0

Example #

• We start by dividing the larger number by the smaller number to get the quotient and remainder:

  54 = 2 × 21 + 12

• Next, we divide the smaller number by the remainder to get another quotient and remainder:

  21 = 1 × 12 + 9

• We repeat the process with the new pair of numbers:

  12 = 1 × 9 + 3

• Finally, we have:

  9 = 3 × 3 + 0

• Since the remainder is now 0, we have found the GCD of the original two numbers. In this case, the GCD of 54 and 21 is 3.

• By replacing the larger number with its remainder by dividing it by the smaller number, we get a smaller pair of numbers. Repeating this process results in progressively smaller pairs of numbers until both numbers are equal.

How it works visually #

• Suppose we have 2 big numbers represented as 2 piles of stones. We are going to find the GCD of the 2 piles of stones.
• Pile B is bigger than A. If we find copies of stones from a smaller pile in the larger pile, we subtract the copies.

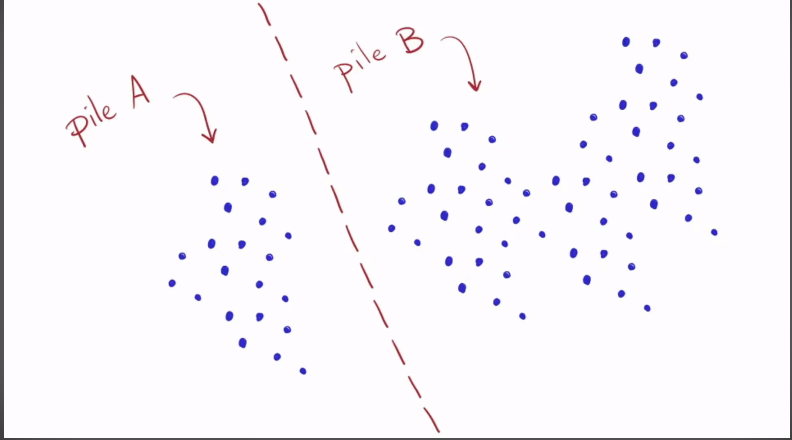
• We start by finding copies of pile A in pile B as shown below.

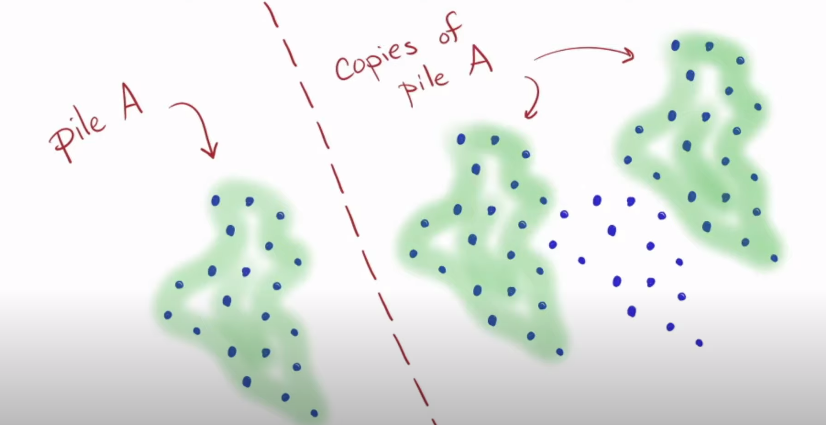
• Subtract the copies from pile B

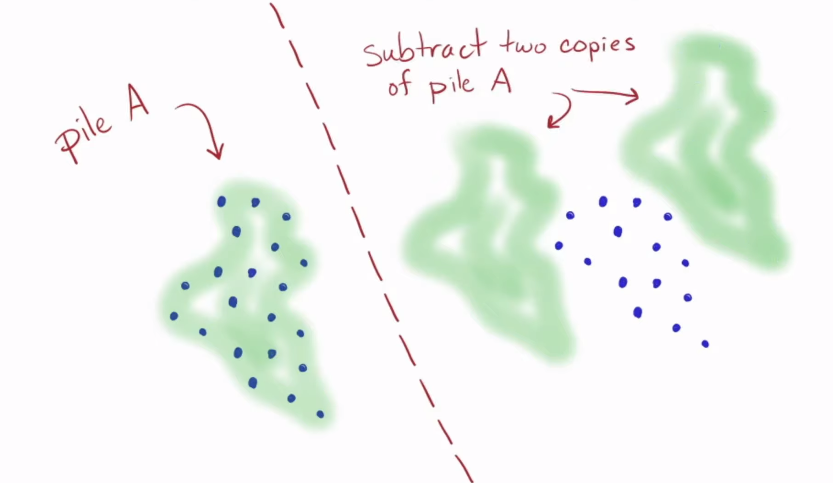
• We end up with the following resulting pile

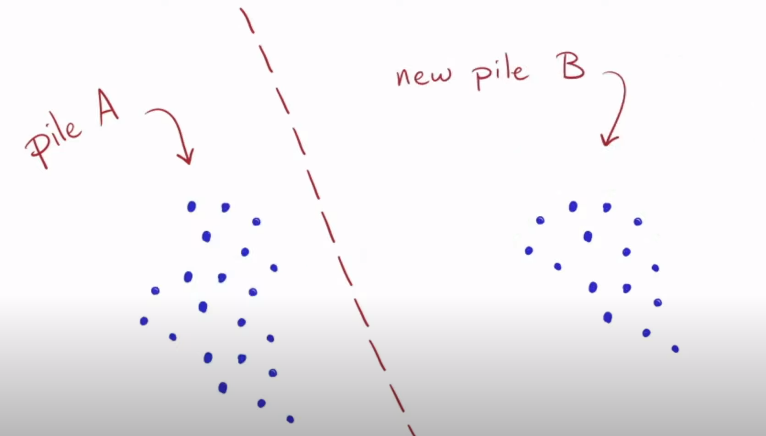
• Pile B is now smaller than A. We find copies of pile B in pile A

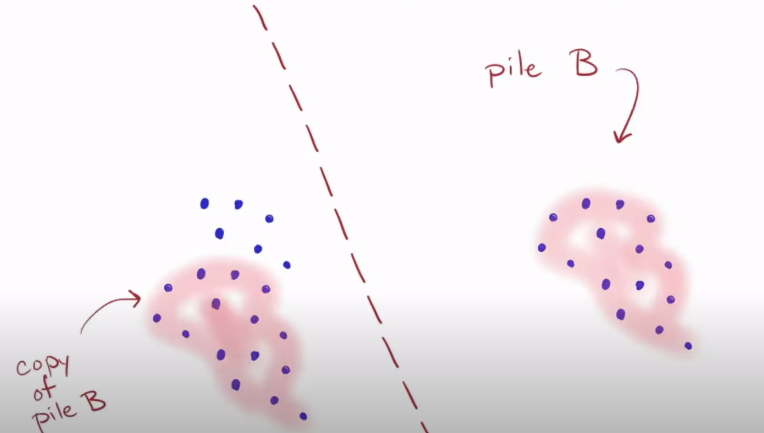
• Subtract the copy of pile B from pile A

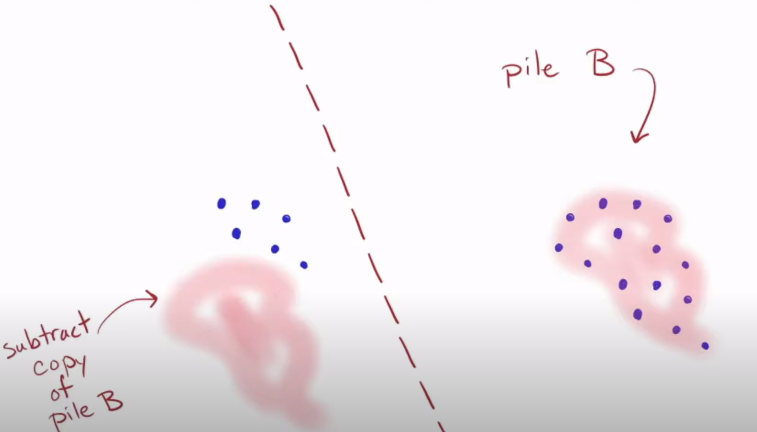
• We end up with the following resulting pile

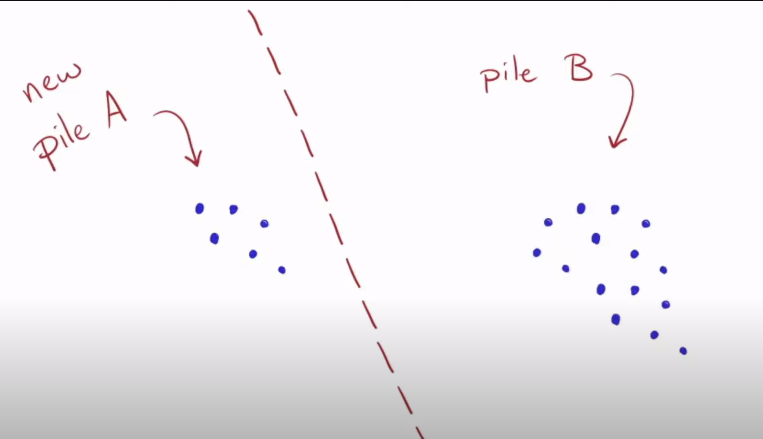
• Pile A is now smaller than B. We find copies of pile A in pile B

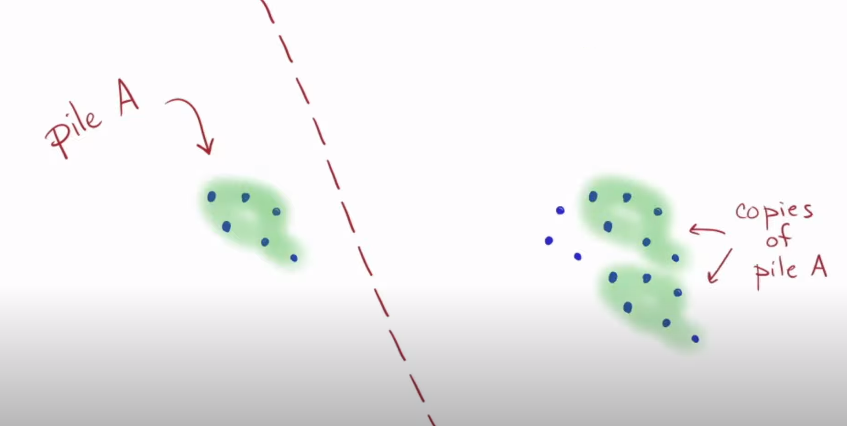
• Subtract the copies of pile A from pile B

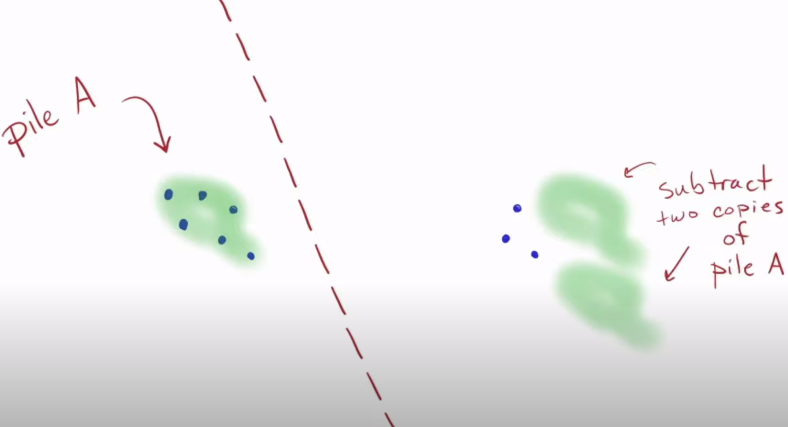
• Find copies of pile B (which is now smaller), in pile A

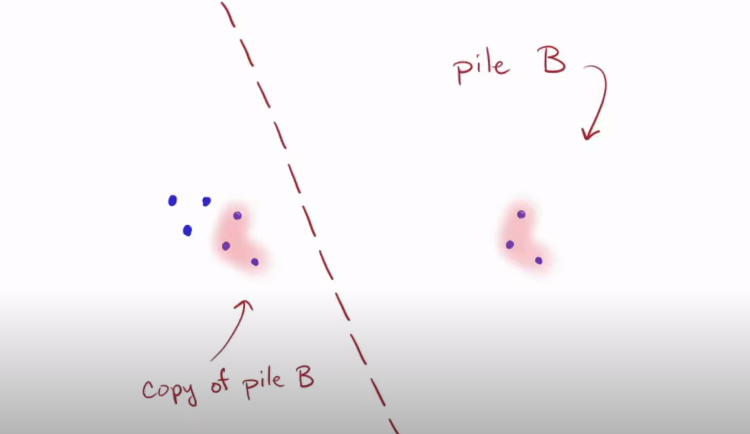
• Subtract the copy

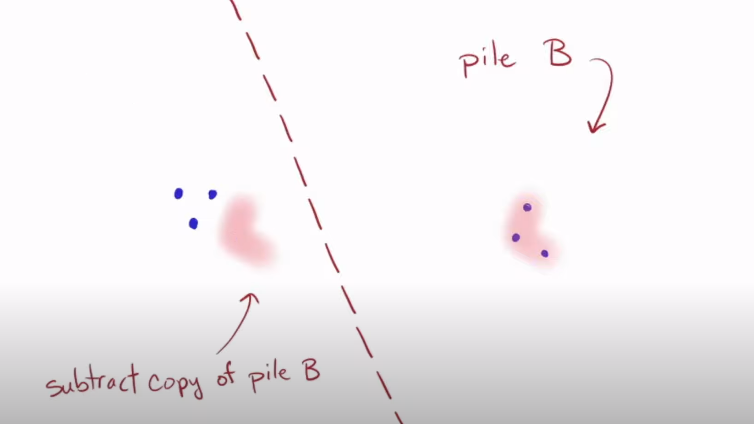
• Now that the 2 piles are equal, it means we have found the GCD which is 3

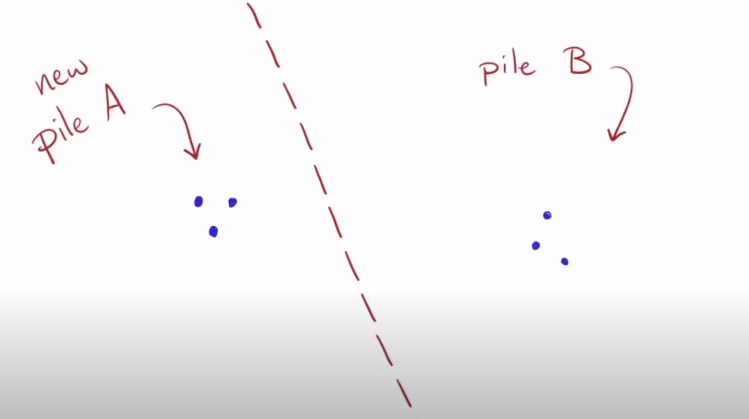
• The 2 numbers representing the pile are 21 and 54 whose GCD is 3

Note

• Repeated subtraction is just a division operation
• We stop our operations when we divide a and b and get a remainder of 0 which means the numbers are either equal or one of the 2 numbers is a 0, making the other number the GCD

The algorithm in python #

Solution #

• We will utilize recursion to break down the large problem into smaller sub-problems and find the solution
• The first step is to come up with a base case. The base case tells us when we should stop our calculation. We saw from the above computations that we stop when the numbers are equal or we get a 0. If b is zero, we have found the GCD of a and b, which is a. Therefore, we return a as the result
• Otherwise, we perform a recursive call when we calculate the remainder of a divided by b using the modulo operator %, and call the gcd function recursively with the arguments b and a % b.
• This operation replaces the larger number with its remainder when divided by the smaller number

Code #

• The following is a short implementation of the algorithm

def main(a,b):

    if b == 0:
        return a
    return main(b,a%b)

print(main(54,21)) #3

Extended Euclidean Algorithm #

• This is an extension to the euclidean algorithm where in addition to the GCD of integers a and b, we compute x and y such that

  ax + by = gcd(a,b)

• The GCD of 54 and 21 is 3.

• The steps used were:

  step 1: 54 = 2 × 21 + 12

  step 2: 21 = 1 × 12 + 9

  step 3: 12 = 1 × 9 + 3

  step 4: 9 = 3 × 3 + 0

• Now we work backward from step 3 (we don’t use step 4 because it has a remainder of 0) to find x and y:

  Step a: 3 = 12 - 1 × 9

  Step b: 3 = 12 - 1 × (21 - 1 × 12) 3 = 2 × 12 - 1 × 21

  Step c: 3 = 2 × (54 - 2 × 21) - 1 × 21

  step d: 3 = 2 × 54 - 5 × 21

• In step a, we substitute the equation from step 3 (12 = 1 × 9 + 3) to express 3 as a linear combination of 12 and 9.

• In step b, we substitute the equation from step 2 (21 = 1 × 12 + 9) to express 3 as a linear combination of 12 and 21

• In step c, we substitute the equations from step 1 to express 3 as a linear combination of 54 and 21. We continue this process until we have expressed the GCD as a linear combination of the original two numbers.

• We end up with 2 and -5 as our coefficients

The algorithm in python #

Solution #

• We perform another recursive algorithm for this case as well. It may seem intimidating but it gets pretty simple once you see how we generate the equations for coming up with the coefficients

• So far, we know that

  ax + by = gcd(a,b)

• The gcd(a,b) can also be rewritten as gcd(b,a%b) which is a recursive operation so:

  ax + by = gcd(b,a%b)

• We can rewrite gcd(b,a%b) in the form ax2 + by2 as shown:

  gcd(b,a%b) = b ⋅ x2 + (a%b) ⋅ y2

• Recall that we said dividend = quotient * divider + remainder.

• In the form of a and b: a = b*q + r where r is a%b and q is a/b

• So, the remainder can be rewritten as remainder = dividend - (quotient * divider).

a%b = a - (a/b) ⋅ b

• Rewrite the remainder

  gcd(b,a%b) = b⋅x2 + [a - (a/b) ⋅ b] ⋅y2

  gcd(b,a%b) = b⋅x2 + a⋅y2 - [a/b ⋅ b] ⋅ y2

• Factor the b

  gcd(b,a%b) = a⋅y2 + b[x2 - (a/b)]⋅ y2

• Replace with the original

  ax + by = a⋅y2 + b[x2 - (a/b)] ⋅ y2

• Solve for x

  ax = a⋅y2

  x = y2

• Solve for y

  by = b[x2 - (a/b)]

  y = [x2 - (a/b)]⋅ y2

• We recursively find x1 and y2 and then find x and 2

Base Case #

• Just like in the euclidean algorithm, we check if one of the numbers between a and b is 0. Suppose b is 0 then:

ax +0y = gcd(a,b) = a

• That results in x = 1 and y = 1

Code #

def extended(a, b):

    if b == 0:
        return (1, 1)
    else:
        x2, y2 = extended(b, a % b)
        y = x2 - (a // b) * y2
        x = y2
        return (x, y)

• You can see how we use the equations we computed to form a base case and recursive algorithm to find our coefficients

Conclusion #

• We have seen how we can compute GCDs of large numbers efficiently using the euclidean algorithm. It is very fundamental in many cryptographic systems and we will see its application in the next blogs.